Can The Average Rate Of Change Of A Function Be Constant

Average Rate of Alter

Key Questions

The average charge per unit of change is constant for a linear role.

Another fashion to country this is that the average charge per unit of change remains the same for the entire domain of a linear role.

If the linear office is #y=7x+12# then the average rate of change is 7 over any interval selected.

Gradient intercept course
#y=mx+b#, where #k# is the slope.
The rate of change is the slope of the graph.

It really doesn't make much sense to try to apply this to nonlinear functions, and you certainly cannot apply an "average" value to a non-linear function unless you first linearize it. Even then, the estimation of what that "average" means must be carefully understood.
Average rate of change is just some other mode of proverb "slope".
For a given part, you tin can take the x-values and apply them to calculate the y-values, then use the slope formula: #thou=frac{y_2-y_1}{x_2-x_1}#

Example: Given the function f(ten) = 3x - viii, find the average rate of modify betwixt 1 and 4.

f(ane) = 3(one) - 8 = -five and f(four) = 3(4) - 8 = 4

m = #frac{4-(-5)}{4-i}# = #frac{9}{3}# = 3 Surprised? No, because that is the slope between Whatsoever two points on that line!

Instance: f(x) = #x^two-3x# , notice the average rate of alter between 0 and 2.

f(0) = 0 and f(2) = iv - 6 = -2

yard = #frac{-2-0}{2-0}# = #frac{-2}{2}# = -1
Since this function is a bend, the average rate of alter between any two points will be different.

Yous would repeat the above procedure in order to discover each unlike slope!

If yous are interested in a more advanced look at "average rate of change" for curves and non linear functions, ask about the Difference Caliber.
The boilerplate charge per unit of change of a office #y=f(10)#, for example, tells you of how much the value of the function changes when #x# changes.

Consider the following diagram:

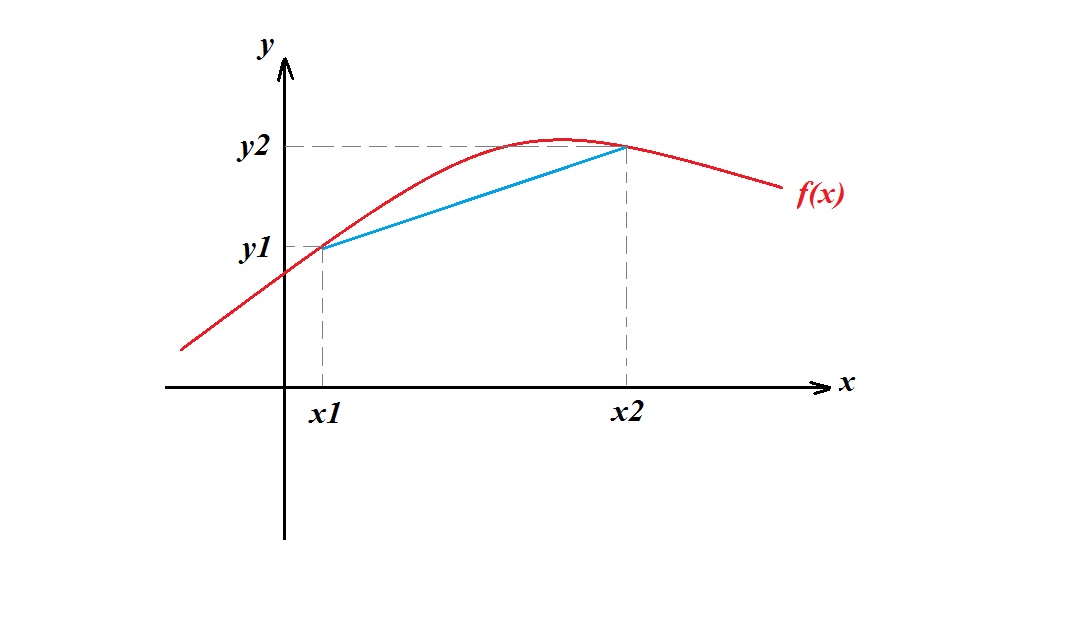
when #x# changes from #x1# to #x2# the value of the part changes from #y1# to #y2#. The average rate of modify volition be:
#(y2-y1)/(x2-x1)# and it is, basically the slope of the blue line.

For example:
if #x1=1# and #x2=5#
and:
#y1=ii# and #y2=10#
you get that:
Boilerplate charge per unit of modify#=(ten-2)/(five-one)=8/iv=2#

This means that for your function: #color(crimson)("every time "x" increases of 1 then "y" increases of 2"#
Manifestly your function is not a perfect straight line and it volition modify differently inside that interval but the average rate can only evaluate the change between the two given points not at each individual indicate.